There is no "if" clause in QC (Quantum circuits cannot control unknown gates)

... then we show that this is barely an inconvenience.

Prerequisites

Basic acquaintance with linear algebra (inner products, eigens, etc.), quantum circuit notation (upto controlled gates), basic familiarity with quantum computing terms.

---

Introduction

Is it possible to construct a fixed quantum circuit, such that if any arbitrary unitary gate is provided as input, the circuit will function as a controlled-U gate?

The paper which will be looked at in this post (Quantum circuits cannot control unknown operations by Mateus Araújo et al.) answers the question, but to get a wider context we shall be looking at some workarounds that do not work, as well as the no-programming theorem. Don’t skip any section which you don’t understand, since every section is connected to the other.
You don’t have to read the paper(s) to follow along the post, however you might find them interesting.

Format of the post:

• Introduction

• Possible workarounds?

• No-Programming Theorem

• Proof of No-Programming Theorem

  • Proving the postulate

• Link to our original objective

• Central proof (of the central paper)

• Surprisingly easy to circumvent (in practical implementations)

• Conclusion

Since this is a long post, you can download the PDF. The PDF is much more direct.
Also, if you’re reading this on the phone then some of the LaTeX expressions might get cut off. Rotate your screen to fix this.

Let’s begin.

---

Possible workarounds?

Is there any way we can work around the problem, such as maybe:

Decomposing the controlled gate within the circuit itself:

Nielsen and Chuang explain¹ how to do the decomposition of a controlled-U gate within a circuit:

Circuit implementing the controlled-U operation for single qubit.

Here, α, A,B,C satisfy U=e^(iα)AXBXC, ABC = I.

The reference goes into more detail (such as why we can write the unitary in this manner in the first place), but we can intuitively see why this works.

The phase term implementation is straightforward-

\(|\psi\rangle (e^{i \alpha}|\phi\rangle)=(e^{i \alpha}|\psi\rangle) |\phi\rangle=e^{i \alpha}|\psi\rangle|\phi\rangle\)

As a result, the gate activates if the first qubit’s component is |1⟩.
If the first qubit is zero, then the gates acting on the second qubit resolve to identity.

This method only works when we have a complete characterization of the unitary gate/its matrix representation.

• Store the unitary gate by passing it as an input:

It is possible to do so quite easily in classical computing. We could store U(its description) as a bitstring in memory, and call it as required, based on the trigger.

One would believe this should be possible for quantum circuits as well; we provide all the information required for “building” the arbitrary unitary U via one set of registers, and the state it must act on via another set of registers. The “master” circuit will then map the first set of qubits to the intended unitary state, after which the operation will be carried out, giving us U|ψ⟩.

The unitary matrix acting on m qubits is a 2^m × 2^m matrix, so roughly 2^2m real numbers are needed to describe the matrix. The number of real numbers needed to represent a 2m qubit state is 2^2m+1-1. (Easily seen: 2^2m possible states, each state’s coefficient is complex (so 2 real numbers), -1 due to the normalization constraint.)

Switching over to classical computing and discrete functions²:
If we say that our input bitstring length is k and the output bitstring length is k as well, then we will require k⋅2^k classical bits to pass the function as an input. The string which encodes the functions will simply be the outputs concatenated into a single string. This becomes clear with an example:

\(\displaystyle{\displaylines{f(00)=10, f(01)=11,f(10)=00,f(11)=11\\ \text{Input string: }10110011}}\)

Crux: If we can do this in classical computing, could we do the same for arbitrary unitary gates? Can we somehow encode arbitrary unitary gates (that maps the input set of qubits to the output set of qubits) as a quantum state?

Spoiler: You can’t. The No-Programming Theorem prevents this.

[Back↑]

---

No-Programming Theorem

Nielsen and Chuang showed³ that this cannot be done in a deterministic manner, but can be achieved probabilistically. Both aspects will be covered in detail.

Briefly, the theorem states that we cannot define a fixed⁴ quantum circuit which takes in a unitary gate U in the form of a state encoded via qubits, say |x⟩, and performs some manipulation so that the U acts on the input state we provide separately.

We first define what do we mean by a fixed circuit.

Formally, given an m-qubit data register⁵ |d⟩ and an n-qubit program register
|P_U⟩ which maps to U, let us assume the existence of a fixed circuit (whose operations are defined by G) such that:

\( |d\rangle \otimes |P_U\rangle \rightarrow G[|d\rangle \otimes |P_U\rangle] \rightarrow U|d\rangle \otimes |P_U '\rangle\)

Our task is to show that G cannot exist.

Before proving the no-go theorem, we need to establish the following:

The output program is independent of the data state:

If the input registers are allowed to be entangled, the unitary applied itself will change based on the data input, making it ill-defined.

We then show |P’_U⟩ does not depend on |d⟩ explicitly:

\(\displaystyle{\displaylines{G[|d_1\rangle \otimes |P_U\rangle] \rightarrow U|d_1\rangle \otimes |P_{U_{1}} '\rangle \\ G[|d_2\rangle \otimes |P_U\rangle] \rightarrow U|d_2\rangle \otimes |P_{U_{2}} '\rangle}}\)

Taking inner product of both, we see that:

\(\langle P_{U_2}'|P_{U_1}'\rangle = 1 \text{ when } \langle d_2|d_1\rangle \neq 1\)

So we have obtained the independence for non-orthogonal data states. We can do for orthogonal states as well by taking an extra state |d₃⟩ that is non-orthogonal to both and using transitivity.

[Back↑]

---

Proof of No-Programming Theorem

(PS. If you find it hard to follow the approach, I’ve summarized it at the bottom of this section.)

Our plan of attack is as follows: We show that for every distinct unitary operation that the fixed circuit must implement, the dimension of the program register must be increased by 1. We show this by proving that distinct unitaries must correspond to orthogonal states.
Once this is done, it’s easy to see the consequence of infinite⁶ unitary gates:

∞ distinct unitary gates, ∞ dimensional system, ∞ qubits. Impossible to implement, for every time the circuit is fixed, its input space must be expanded.

Before we prove the statement in the first paragraph, let us first establish that it is atleast possible to have a fixed circuit that can implement a finite number of distinct unitary gates, depending on the program state |P⟩.

Formally, we must see if a program register of dimension ‘n’ can deterministically implement ‘n’ distinct⁷ unitary operations (ignoring global phase) on the data register via control gates.

It is possible. We show this (informally)⁸ via explicit construction.

Expanded for simplicity. First two qubits correspond to the program register. Description allows one to implement unitary operators depending on the state of the program register, thus making it one possible implementation of the fixed circuit.

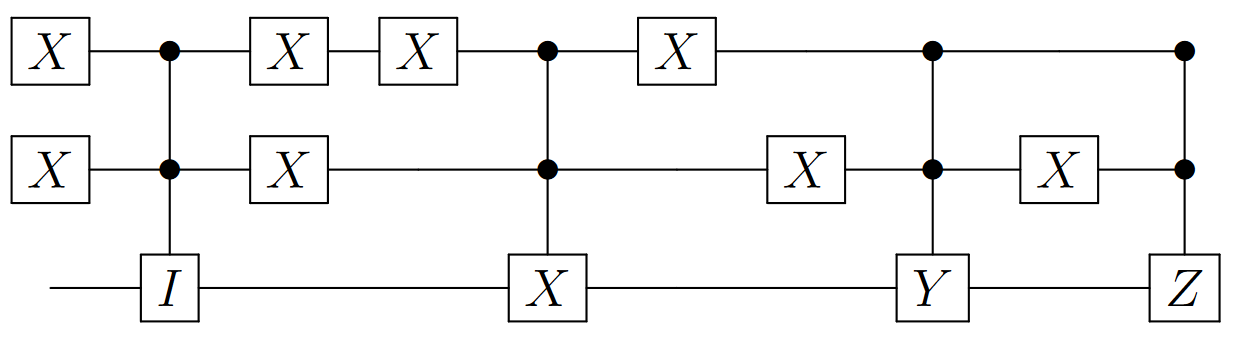
The circuit above does it for n=4. It’s straightforward⁹ to see how it works. 00→I, 01→X, 10→Y, 11→Z (Little-endian notation is followed.)

Next, we postulate that if a fixed circuit is a deterministic implementation and implements {U₁, U₂, ..., U_n}, then the following must hold:

\( \text{ The program states } |P_{U_{1}}\rangle,...,|P_{U_{n}}\rangle \text{ are orthogonal}\)

If this holds, then the program register is atleast n dimensional and occupies log₂(n) qubits.

[Back↑]

We now shall prove this postulate holds via contradiction.

---

Let us assume that the above postulate does not hold. Let |P⟩ and |Q⟩ implement U_P and U_Q which are distinct, but the states themselves are not orthogonal.

\(\displaystyle{\displaylines{G[|d\rangle \otimes |P\rangle] \rightarrow U_{P}|d\rangle \otimes |P'\rangle \\ G[|d\rangle \otimes |Q\rangle] \rightarrow U_{Q}|d\rangle \otimes |Q'\rangle}}\)

Taking inner product:

\(\langle Q|P \rangle=\langle Q'|P'\rangle\langle d|U_{Q}^{\dagger}U_{P}|d\rangle\)

Assume ⟨Q′|P′⟩ ≠ 0. Then the following must hold:

\(\displaystyle{\displaylines{\frac{\langle Q|P\rangle}{\langle Q'|P'\rangle}=\langle d|U_{Q}^{\dagger}U_{P}|d\rangle}}\)

LHS is not dependent on |d⟩. As seen earlier: numerator and denominator are independent, so RHS must be a constant value.

For RHS to be constant:

\(\displaystyle{\displaylines{U^{\dagger}_Q U_P= \text{constant}*\mathbb{I}}}\)

But this contradicts our initial condition that U_P and U_Q are distinct.¹⁰ So the only other resolution is to say our initial assumption ⟨Q′|P ′⟩ ≠ 0 is wrong.¹¹

This implies that ⟨Q′|P′⟩ = 0. Since this is true, LHS must be 0 as well, ie. ⟨Q|P⟩ = 0.
Hence proven.

From this, the rest follows. A fixed circuit will have to implement an infinite number of unitary gates. This would require it to be able to take an infinite number of orthogonal states as input, which is impossible for a fixed circuit.

Thus, we cannot have a fixed circuit can deterministically implement all possible unitary matrices.

Just to summarize what we’ve done here:

1. We establish a plan of attack- if we can show that distinct unitaries must correspond to orthogonal program states, then the no-programming theorem is a byproduct of the statement.

2. We see if it’s even possible to create a fixed circuit that can do this for a finite set of distinct unitaries. We show that it is possible to do so.

3. We now add an additional condition onto (2.) that the corresponding program states must be orthogonal (this is just restating 1.)

4. We prove the validity of 1. through contradiction.

   1. Assume the program states corresponding to distinct unitaries are non-orthogonal.

   2. We obtain the unitaries are not distinct. Since this isn’t possible, (1.) is proven by contradiction.

5. No-Programming theorem is the byproduct.

[Back↑]

---

A probabilistic implementation is possible

Quite surprisingly, a probabilistic implementation is possible!

Implementation for a 1-qubit input unitary.

The following procedure has only been described for one qubit, but a generalization is possible (see footnote 3).

Although the setup looks exotic, it still essentially works on the same principle as the Quantum Teleportation protocol. If you don’t know about it, then N&C¹² gives a pretty good explanation of how the protocol works.¹³

The above programmable quantum gate array functions as follows: The data qubit upon which the unitary is applied is |d⟩. The Bell state |Φ⁺⟩ is prepared, out of which one is passed as input to the unitary. The data qubit and the remaining Bell state qubit are jointly measured. In the end, we perform a SWAP operation between the data qubit and the Bell state qubit on which the unknown unitary acts.

It is straightforward to see what |P_U⟩ is:

\(|P_U\rangle = \frac{|0\rangle U|0\rangle+|1\rangle U|1\rangle}{\sqrt{2}}\)

This will be the state that will effectively encode U into the gate array G.
If we define the data qubit as |d⟩= α|0⟩ + β|1⟩, our combined state |d⟩⊗)|P_U⟩ becomes:

\(|d⟩\otimes|P_U⟩=[\alpha|0\rangle + \beta|1\rangle] \frac{|0\rangle U|0\rangle + |1\rangle U|1\rangle}{\sqrt{2}}\)

Through algebraic manipulation we can rewrite the combined state:

\(|d⟩\otimes|P_U⟩=\frac{1}{2} \big[ |\Phi^+\rangle (U|d\rangle) + |\Phi^-\rangle (U\sigma_z|d\rangle) + |\Psi^+\rangle (U\sigma_x|d\rangle) + i|\Psi^-\rangle (U\sigma_y|d\rangle) \big]\)

(Following Bell state convention.)

Now, by performing Bell measurements¹⁴ on the first two qubits, we can discern the state of the unmeasured qubit. With probability ¹/₄ we see that the unitary has been correctly applied on the data qubit! The other three obtained cases cannot be used. For example, if the measurement corresponds to Uσ_X|d⟩, the circuit has implemented the unitary Uσ_X instead of U thus “failing”.

As stated earlier, the probabilistic implementation can be seen as a direct consequence of the quantum teleportation protocol:

The left hand side is just the quantum teleportation circuit, but with the additional modification of applying the unitary gate at the end of the unmeasured qubit. Since we already know the correspondence without the unitary…

\(\begin{array}{c c} \textbf{Measurement outcome} & \textbf{Expression} \\ \hline 00 & \alpha |0\rangle + \beta|1\rangle \\ 01 & \alpha |1\rangle + \beta|0\rangle \\ 10 & \alpha |0\rangle - \beta|1\rangle \\ 11 & \alpha |1\rangle - \beta|0\rangle \\ \end{array}\)

... it becomes straightforward to determine the output after the application of the unitary.
We can now shift around the unitary applied on the third qubit since rest of the operations (incl. the measurements) only concern the first two qubits.

Just to make it clear, we must here reiterate the objective of the fixed circuit, which is to send a state into the gate array such that the unitary corresponding to the state is then applied onto the data qubit.

Therefore, trivial implementations such as the one below do not count:

G here is simply the identity gate.

Nevertheless, one is still allowed to apply the arbitrary unitary onto any state which is then fed into the system, since only the definition of a fixed circuit needs to be satisfied.

Unfortunately the probability of success is given by 2^-2m in its generalized case, so it does not scale well.

[Back↑]

---

Link to our original objective

Now that these workarounds have been shown to be impossible, this leaves us with the only¹⁵ option of inserting the unknown gate as a variable directly into the circuit.

From this itself, we can provide an informal argument as to why a universal circuit is impossible:
Let us say that we are given U and e^iϕU. They are essentially the same operator except for the global phase. Such an operator can be plugged in anywhere, and it would not make a difference except for changing the global phase of the qubit.
For controlled-U, the global phase now plays a measurable role.

\(\text{Control-}\mathbb{I}=\mathbb{I}\otimes\mathbb{I}, \ \text{Control-}(\mathbb{-I})=\text{Control-}Z\)

Thus, the circuit will now have to quantify the global phase, a non-measurable quantity.¹⁶
We need to show that the initial problem holds for control-e^iuU as well, since we generally neglect global phase. There are cases where such phase dependencies occur.
From the paper itself:

Note also that if one's goal in implementing the control-U is to measure the energy of a Hamiltonian such that U=e^iHt via phase estimation, the fact that this global phase is arbitrary is equivalent to the fact that one can apply an arbitrary shift to the spectrum of the Hamiltonian.

[Back↑]

---

Central proof (of the central paper)

The proof of impossibility is as follows:

Figure from paper. First line is taken to be ancilla/“a”-dimensional quantum system.

We try to find unitaries A and B to implement a controlled-U such that the equality holds for any possible U.

Control-U gate: I_d⊕U. For a system composed of qubits, it means that the control-U gate is controlled by log₂d qubits.

Let the total system be a+j dimensional. The following equality must be proven:

\(B(\mathbb{I}_a\otimes \mathbb{I}_2 \otimes U)A|0\rangle_{a}|\psi\rangle_j=W_U|0\rangle_a(\mathbb{I}_d\oplus e^{iu}U)|\psi\rangle_j\)

Additional points:

• Let W_U|0⟩_a = |U*⟩_a to simplify notation.

• We must take the tensor product with a two-dimensional Hilbert space as well, as it ensures that the resultant will have some subspace to use as control.

• For the proof here, we assume only one qubit as the control gate. Result can be

  generalised.

Since every unitary gate can be decomposed into a linear combination of Pauli gates,¹⁷ let us consider the cases where U is X gate, Z gate, and for the gate G = αX + βZ. (Normalized coeffs.)
This is a different G. It is not the same one referred to in the No-Programming Theorem.

Then:

\(B[\mathbb{I}_{a}\otimes\mathbb{I}_{2}\otimes G] A (| 0\rangle_{a}|\psi\rangle_{j}) = W_{G}| 0\rangle_{a}\left( \mathbb{I}_{2}\oplus e^{ig}G \right) |\psi\rangle_{j}\)

\(B\lbrack \mathbb{I}_{a}\otimes\mathbb{I}_{2}\otimes(\alpha X + \beta Z)\rbrack A (|0\rangle_{a} |\psi\rangle_{j}) = W_{G}| 0\rangle_{a}\left( \mathbb{I}_{2}\oplus e^{ig}G \right) |\psi\rangle_{j}\)

\(\alpha W_{X}| 0\rangle_{a}\left( \mathbb{I}_{2}\oplus e^{ix}X \right)|\psi\rangle_{j} + \beta W_{Z}\left| 0\rangle_{a}\left( \mathbb{I}_{2}\oplus e^{iz}Z \right) \right|\psi\rangle_{j} = W_{G}\left| 0\rangle_{a}\left( \mathbb{I}_{2}\oplus e^{ig}G \right) \right|\psi\rangle_{j}\)

Taking the inner product with |G*⟩_a and tracing out the j-dimensional subspace:

\(\alpha\langle G^{*}| X\rangle_{a} + \beta\langle G^{*}|Z\rangle_{a} = 1\)

Similarly, inner product with |G*⟩_a|ψ⟩_j gives:

\(\alpha\langle G^{*}| X\rangle_{a} \: e^{ix}\langle\psi|X\left| \psi\rangle_{j} + \beta\langle G^{*} \right|Z\rangle_{a}\: e^{iz}\langle\psi|Z|\psi\rangle_{j} = e^{ig}\langle\psi|\alpha X + \beta Z|\psi\rangle_{j}\)

Since X and Z are orthogonal, it is necessary that ⟨G*|X⟩= e^i(g-x) and ⟨G*|Z⟩= e^i(g-z) .

If we substitute this into the equation obtained after the partial trace, we get:

\(e^{i(g-x)}(\alpha + \beta e^{i(x-z)})=1\)

Taking the modulus squared of the equation shows that cos(x-z)=0. Repeating this same procedure with gates X, Y, αX + βY and Y, Z, αY + βZ:

\(cos(x-z)=cos(x-y)=cos(y-z)=0\)

No such set of {x, y, z} exists.

Thus, the transformation is not possible. No such circuit can be constructed.

Hence proved.

[Back↑]

---

Surprisingly easy to circumvent (in practical implementations)

The now-proven theorem only holds when U belongs to the universal set of unitary gates. If even one eigenvector of U is known, then we can construct a circuit that performs its control.

Zhou et al.¹⁸ provide a fairly simple way of circumventing the theorem we just proved.
This is achieved by trivially extending the Hilbert space of the unknown unitary's input, such that there is a subspace over which the unitary acts, and a subspace over which it doesn't.
Thus, given an arbitrary unitary, we can plug it into the circuit and control it using an extra qubit.
This will become clearer with explicit constructions.

Zhou et al. state two methods of extension:

• Increasing the dimension of the target register: The target register now (instead of being a set of qubits) is a set of qudits, each qudit being a four-level system with logical states |0⟩, |1⟩, |2⟩ and |3⟩. The action of each X_α gate is to swap the states in the manner below:

  \(X_\alpha|0\rangle = |2\rangle, X_\alpha|1\rangle = |3\rangle, X_\alpha|2\rangle = |0\rangle, X_\alpha|3\rangle = |1\rangle\)

  The unitary only acts on states |2⟩ and |3⟩, and for the rest it acts as identity.

  

  Example shown for a unitary acting on 3 qudits.

• Increasing the number of qubits: Each original qubit that was being acted upon by the unitary is now accompanied by an ancillary qubit. The circuit conditionally shifts the states into and out of the circuit.

  

  Example shown for a unitary acting on 2 qubits. The box X gate represents the SWAP gate. |A₁⟩ and |A₂⟩ play the role of ancillary qubits.

Zhou et al. state that the first implementation is more suitable for the present usage, as it uses smaller separate qubits, and the existing technologies are sufficient to scale the system for larger input unitaries.

The authors of the original paper under focus (Araújo et al.) use the first implementation in their paper, and also provide a photonic implementation of circumvention:

(Araújo et al.) Interferometer that controls a qudit blackbox U. Here the control qubit is the polarization of the photon, and U acts on some additional degree of freedom of the same photon. The PBSs are polarizing beam splitters. A photon with polarization |H⟩ takes the lower path (in red), while one with polarization |V⟩ takes the upper path (blue).

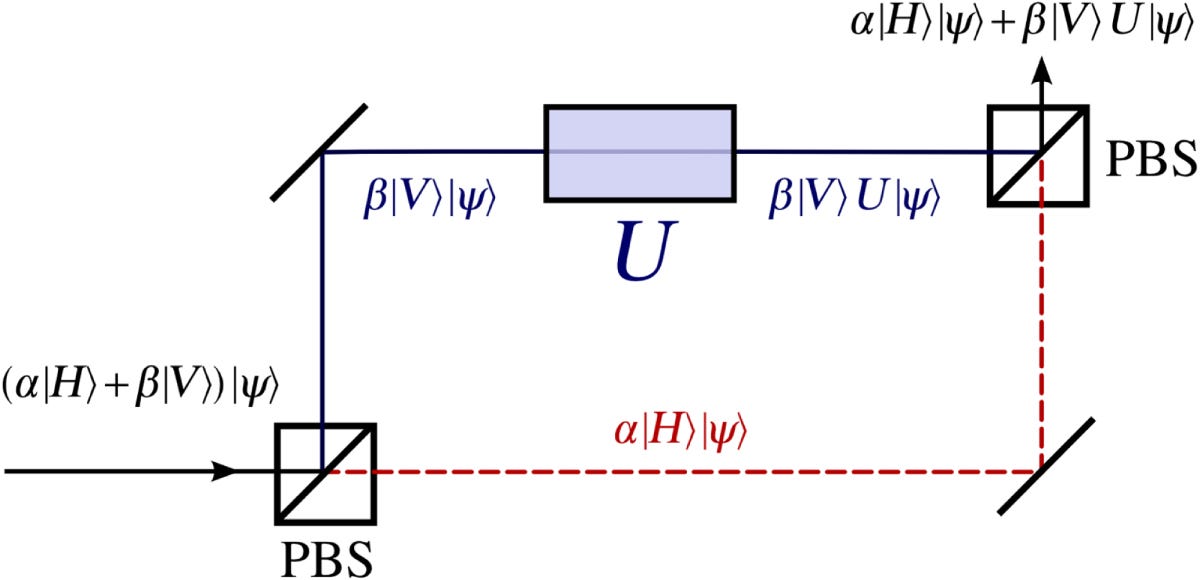
The phase shift operation is an example of an operation that does not affect the polarization of the photon.

This can be scaled to multi-qubit unitaries as well:

Scalable implementation. The control state is encoded in terms of the polarization of n photons as the state α|H...H⟩ + β|V...V⟩.

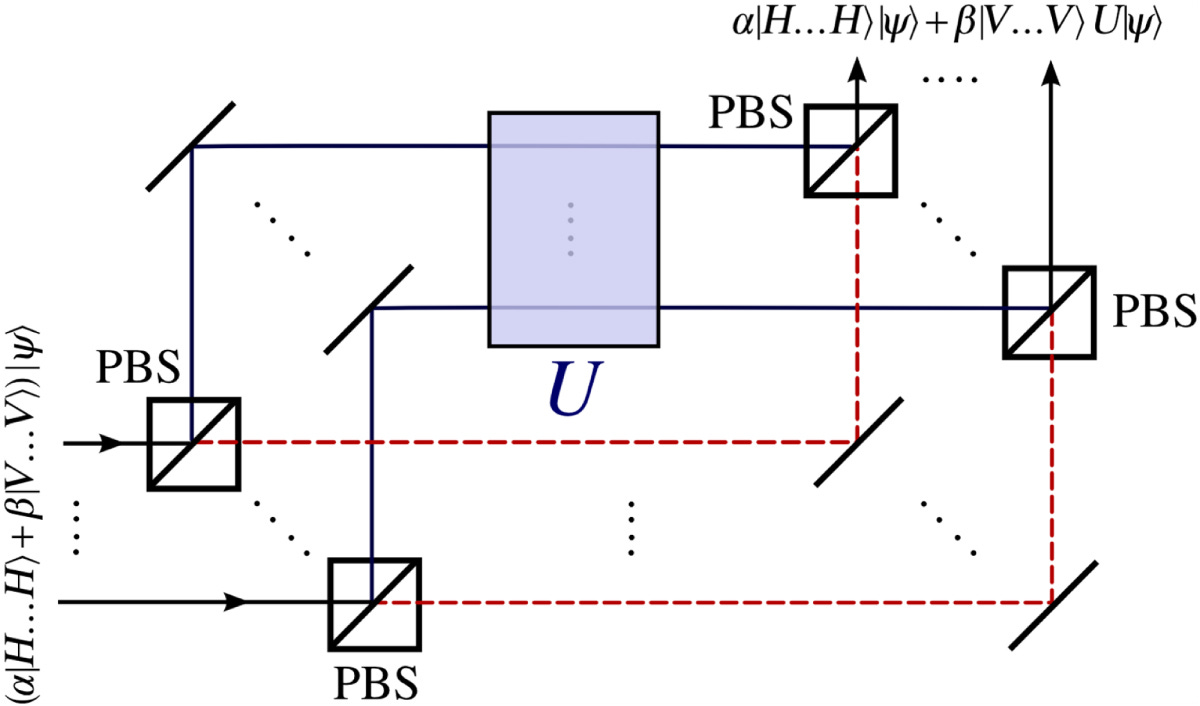
The extended unitaries in these examples have a simple representation:

\(U_\text{physical}=\begin{bmatrix} \mathbb{I}_d & 0 \\ 0 & U \end{bmatrix}\)

[Back↑]

---

Conclusion

The authors argue that since the no-go theorem can be circumvented by any possible physical implementation, the quantum circuit model is incomplete. Such a circumvention must be covered “naturally” by the model if it is to represent quantum physics in its entirety.

It makes sense as well: Let us say genetics forbade any creature from having different colour irses, but your street cat has complete heterochromia.
You’d then have to determine whether there is a workaround possible within the current framework of genetics to explain the phenomena. If a workaround is possible, then there must be a way to modify the framework such that we don’t obtain the “forbiddance” in the first place.

---

The End.

I hope you found this article helpful. Let me know about any points which I’ve interpreted wrongly or overlooked in the comments. I’d appreciate your observations and insights as well!

---

1. M. A. Nielsen and I. L. Chuang, Quantum Computation and Quantum Information: 10th Anniversary Edition. Cambridge: Cambridge University Press, 2010: Page 181

2. Note that even though irrational numbers cannot be described precisely in binary (or any base), it plays no role here. All we are concerned with is describing a function that maps one set of bits to another set of bits, and seeing if we can represent the function as a bitstring as well. We then attempt to do the same with qubits.

3. Nielsen, M. A., and Isaac L. Chuang. “Programmable Quantum Gate Arrays.” Physical Review Letters 79, no. 2 (July 14, 1997): 321–24.

4. By ‘fixed’, we mean that there is some quantum circuit we have designed using gates, such that once this design is fixed, we cannot change it. It prevents us from changing the circuit on a case-by-case basis. It is similar to defining a Universal Turing Machine that takes a Turing Machine and the starting string as inputs.

5. ‘Register’ simply refers to a specific set of qubits.

6. The most straightforward way of seeing this is to consider a 2-D diagonal matrix with the constraint |M₀₀|² + |M₁₁|² = 1. Two parameters, one constraint.

7. Those which cannot be written as some combination of the other chosen unitary matrices.

8. See this paper for a more formal proof of the above statement. The construction argument isn’t from any of the papers, but I can’t see why it shouldn’t be valid. The space of Hermitian n × n matrices are spanned by n² matrices, which is exactly what is happening here. Let me know if this isn’t satisfactory.

9. Exercise: How will you implement the Hadamard gate?

10. Product of two matrices is identity only if they are inverses, or they are the same matrix. Since unitary matrices are their own inverse, they must be the same matrix (disregarding the scaling).

11. We arrive at this conclusion since one of the statements is a given condition and the other is a hypothesis.

12. M. A. Nielsen and I. L. Chuang, Quantum Computation and Quantum Information: 10th Anniversary Edition. Cambridge: Cambridge University Press, 2010: Page 26

13. Why does the protocol work? Why does it give us the answers that it does, instead of giving absolute gibberish when the qubits are measured? I don’t know. The algebraic manipulation seems magical to me. Eg. For double slit, doing the calculations gives us the pattern. The theoretical explanation is constructive and destructive interference. A similar form of answer seems to be missing for the protocol, apart from left field explanations.

14. This is simply using projective measurements (N&C: Pg 87) where the projectors are the made of the outer products of each Bell state with itself, ie. |Φ⁺⟩⟨Φ⁺|, and so on. Alternatively, we can simply invert the procedure given in N&C: Pg 26 and measure in the computational basis to discern what Bell pair we measured.

15. We say this with the exception of the probabilistic implementation case. The authors seem to only be concerned with the deterministic outcome of the no-programming theorem.

16. Exercise: Determine whether it is possible to do so.

17. My handwavy argument in footnote 8 should hold, but there is a cleaner proof in Exercise 2.72 of N&C.

18. Zhou, Xiao-Qi, Timothy C. Ralph, Pruet Kalasuwan, Mian Zhang, Alberto Peruzzo, Benjamin P. Lanyon, and Jeremy L. O’Brien. “Adding Control to Arbitrary Unknown Quantum Operations.” Nature Communications 2, no. 1 (August 2, 2011): 413.